算法分析课程博客分享 13

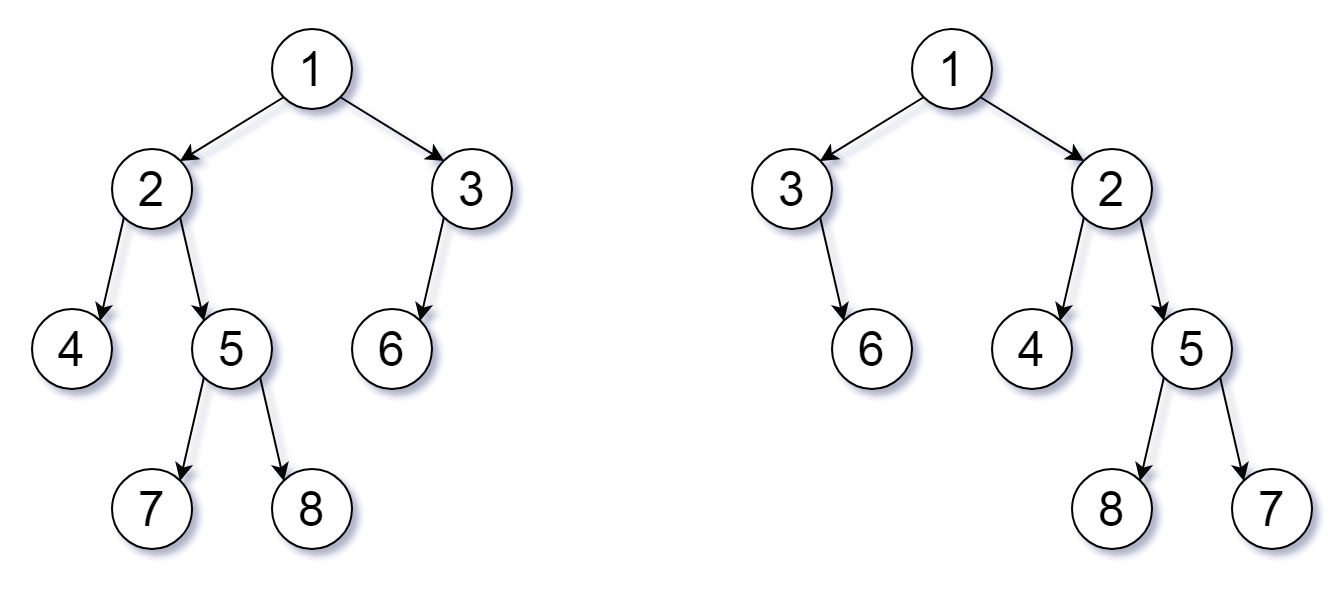
951. 翻转等价二叉树(Flip Equivalent Binary Trees)

示例：
输入：root1 = [1,2,3,4,5,6,null,null,null,7,8], root2 = [1,3,2,null,6,4,5,null,null,null,null,8,7]
输出：true
解释：We flipped at nodes with values 1, 3, and 5.

提示：

每棵树最多有 100 个节点。
每棵树中的每个值都是唯一的、在 [0, 99] 范围内的整数。

解题思路:
首先，如果两棵树是翻转等价的，他们的节点数目一定是相同的。我们用递归的方式检查两棵树是否翻转等价，如果当前节点的值不相等，则可以确认两棵树不是翻转等价的，否则，我们要确认他们的子树是否翻转等价。要确认他们的子树是否翻转等价，我们需要考虑两种情况：进行翻转或者不进行翻转。具体代码如下：

bool flipEquiv(TreeNode* root1, TreeNode* root2) {
    if (root1 == NULL && root2 == NULL)
        return true;
    if (root1 == NULL || root2 == NULL)
        return false;
    if (root1->val != root2->val)
        return false;

    return (flipEquiv(root1->left, root2->right) && flipEquiv(root1->right, root2->left)) || 
           (flipEquiv(root1->left, root2->left) && flipEquiv(root1->right, root2->right));
}

942. 增减字符串匹配(DI String Match)

给定只含 “I”（增大）或 “D”（减小）的字符串 S ，令 N = S.length。

返回 [0, 1, …, N] 的任意排列 A 使得对于所有 i = 0, …, N-1，都有：

如果 S[i] == “I”，那么 A[i] < A[i+1]
如果 S[i] == “D”，那么 A[i] > A[i+1]

示例 1：
输出：”IDID”
输出：[0,4,1,3,2]

示例 2：
输出：”III”
输出：[0,1,2,3]

示例 3：
输出：”DDI”
输出：[3,2,0,1]

提示：

1 <= S.length <= 1000
S 只包含字符 “I” 或 “D”。

解题思路:
通过观察，我们能发现可以通过贪心的方法去解决这个问题。当扫描到 I 时，说明当前数必须小于下一个数，则我们把当前数赋值为未使用的最小的数；当扫描到 D 时，说明当前数必须大于下一个数，则我们把当前数赋值为未使用的最大的数。具体代码如下：

vector<int> diStringMatch(string S) {
    vector<int> res;
    int I = 0, D = S.length();
    for (char c : S) {
        if (c == 'I')
            res.push_back(I++);
        else
            res.push_back(D--);
    }
    res.push_back(S.back() == 'I' ? I : D);

    return res;
}

944. 删列造序(Delete Columns to Make Sorted)

给定由 N 个小写字母字符串组成的数组 A，其中每个字符串长度相等。

选取一个删除索引序列，对于 A 中的每个字符串，删除对应每个索引处的字符。所余下的字符串行从上往下读形成列。

比如，有 A = [“abcdef”, “uvwxyz”]，删除索引序列 {0, 2, 3}，删除后 A 为[“bef”, “vyz”]， A 的列分别为[“b”,”v”], [“e”,”y”], [“f”,”z”]。（形式上，第 n 列为 [A[0][n], A[1][n], …, A[A.length-1][n]）。

假设，我们选择了一组删除索引 D，那么在执行删除操作之后，A 中所剩余的每一列都必须是非降序排列的，然后请你返回 D.length 的最小可能值。

示例 1：
输入：[“cba”, “daf”, “ghi”]
输出：1
解释：
当选择 D = {1}，删除后 A 的列为：[“c”,”d”,”g”] 和 [“a”,”f”,”i”]，均为非降序排列。
若选择 D = {}，那么 A 的列 [“b”,”a”,”h”] 就不是非降序排列了。

示例 2：
输入：[“a”, “b”]
输出：0
解释：D = {}

示例 3：
输入：[“zyx”, “wvu”, “tsr”]
输出：3
解释：D = {0, 1, 2}

提示：

1 <= A.length <= 100
1 <= A[i].length <= 1000

解题思路:
我们要求 D.length 的最小可能值，即求 A 中所有升序排列的列数。我们将列数作为外循环，每次循环中遍历行数，即可求出升序排列的列数。具体代码如下：

int minDeletionSize(vector<string>& A) {
    int res = 0;
    for (int i = 0; i < A[0].size(); ++i) {
        for (int j = 1; j < A.size(); ++j) {
            if (A[j][i] < A[j-1][i]) {
                ++res;
                break;
            }
        }
    }

    return res;
}