算法分析课程期末项目
Capacitated Facility Location Problems
Suppose there are n facilities and m customers. We wish to choose:
- (1) which of the n facilities to open
- (2) the assignment of customers to facilities
- The objective is to minimize the sum of the opening cost and the assignment cost.
- The total demand assigned to a facility must not exceed its capacity.
Preparation
有关 CFLP 的详细内容可以参考以下文件。
首先,我们需要从 Instances 中读取数据。
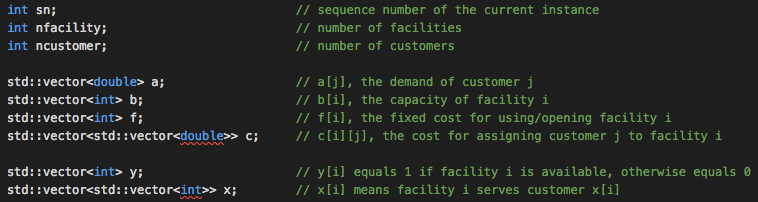
我们使用如图所示的容器保存每个实例的相关数据,并用如下代码读取数据。
bool Solver::load() {
try {
string path = "Instances/p" + to_string(this->sn);
ifstream fin(path);
fin >> this->nfacility >> this->ncustomer;
this->b = this->f = vector<int>(this->nfacility);
for (int i = 0; i < this->nfacility; ++i) {
fin >> this->b[i] >> this->f[i];
}
this->a = vector<double>(this->ncustomer);
for(int i = 0; i < this->ncustomer; ++i) {
fin >> this->a[i];
}
this->c = vector<vector<double>>(this->nfacility, vector<double>(this->ncustomer));
for (int i = 0; i < this->nfacility; ++i) {
for (int j = 0; j < this->ncustomer; ++j) {
fin >> this->c[i][j];
}
}
this->y = vector<int>(this->nfacility, 1);
} catch(exception e) {
cerr << "Failed to load the target" << endl;
return false;
}
return true;
}
Solution 1 (Greedy Algorithm)
对于这种问题,最容易想到的方法就是贪心算法。我们使用如下策略进行贪心。
- 当 y[i] 等于 1 时,代表设施 i 是可选择的设施;当 y[i] 等于 0 时,代表设施 i 是不可选择的设施。
- 把一个需求分配到一个设施时,待分配设施的容量必须大于等于当前需求。
- 顺序扫描所有的客户需求,使用贪心的策略把当前的需求分配到一个可选择的设施,分配时忽略开设设施的开销,把需求分配到拥有最小分配开销的设施。
在观察分析了 Instances 中的各个实例数据后,我发现单个分配开销的值与单个开设开销的值多数比较接近。考虑到需求的数目远比设施的数目要多,我们可以在贪心的时候忽略开设设施的开销,仅在算法最后加上开设设施的开销。这种贪心的策略往往只能找到局部最优解,在某些情况下,甚至会出现无法求出解的情况。当我们贪心地去分配需求时,如果我们没办法分配完所有的需求,我们就返回 cost == -1,通过返回一个无效值表示无法通过贪心算法求解。
pair<double, double> Solver::greedy(bool init) {
if (init && !Solver::load()) {
return make_pair(-1.0, -1.0);
}
struct timeb t0, t1;
ftime(&t0);
double cost = 0.0;
vector<int> capacity = this->b;
this->x = vector<vector<int>>(this->nfacility);
for (int j = 0; j < this->ncustomer; ++j) {
int best_facility = -1;
double best_cost = DBL_MAX;
for (int i = 0; i < this->nfacility; ++i) {
if (this->y[i] && capacity[i] >= this->a[j] && this->c[i][j] < best_cost) {
best_facility = i;
best_cost = this->c[i][j];
}
}
if (best_facility == -1) {
if (init) {
cerr << "Failed to solve with greedy" << endl;
}
return make_pair(-1.0, -1.0);
} else {
capacity[best_facility] -= this->a[j];
cost += best_cost;
x[best_facility].push_back(j);
}
}
ftime(&t1);
string status = "";
for (int i = 0; i < this->nfacility; ++i) {
if (this->x[i].empty()) {
status += "0 ";
} else {
status += "1 ";
cost += this->f[i];
}
}
if (init) {
string path = "Results/p" + to_string(this->sn);
ofstream fout(path);
fout << fixed << setprecision(1) << cost << endl;
fout << status << endl;
for (int i = 0; i < this->nfacility; ++i) {
fout << x[i] << endl;
}
fout.close();
}
return make_pair(cost, (t1.time-t0.time)+(t1.millitm-t0.millitm)*1e-3);
}
我们把贪心算法得到的分配方案以邻接链表的形式保存在 x 中,即使用 x[i] 来保存设施 i 服务的客户。在得到 x 后,我们扫描 x,如果 x[i] 不为空的话,代表我们使用了这座设施,则我们需要令总开销加上 f[i],即开设设施 i 的开销。在应用贪心算法时,我把所有的设施都设成了可选择,这个操作能加大成功求出解的概率,但是这种选择往往不能获得比较好的分配方案。
实验结果保存在以下文件夹中。
简略的结果表保存在以下文件中。
Solution 2 (Tabu Search)
贪心算法时无法获得比较好的方案的,对于这种 NP-hard 问题,我们往往使用启发式算法来获得更好的结果。通常,我们会使用拉格朗日启发式算法、退火算法、禁忌搜索等算法解决这类 Single Source Capacitated Facility Location Problem。在此,我们在贪心算法的基础上应用禁忌搜索来优化我们的算法。
同样地,我们用 make_pair(-1.0, -1.0) 来表示无解的情况。我们先使用默认的贪心算法来获得一组初始解,然后我们把全局最优开销 – global_cost、全局最优 y – global_y、全局最优 x – global_x 设置成使用贪心算法获得的初始解。接下来,我们定义禁忌表 ts 来保存访问过的状态,防止陷入循环中。通常,我们是需要给禁忌表设置一个最大长度的,但由于我把最大迭代次数设成了 100,而实际上的可能性数目十分庞大,我们即便不设置禁忌表的最大长度也不会有问题。我们通过计算最优的 local_cost 来搜索出较优解。在每一次迭代中,我们先把 local_cost 初始化成一个无效值,这里使用的是 DBL_MAX。接下来,我们把禁忌算法的领域定义为改变一个设施的可选择状态,即每次只改变 y 的其中一个值。我们基于邻居 y’ 使用贪心算法算出一组邻居解,然后我们比较这组解的 cost 与 local_cost 的值,当 cost < local_cost 且邻居 y’ 不在禁忌表中时,我们更新 local_cost 的值。而禁忌搜索还存在特赦规则,即满足某种条件时,即便 y’ 在禁忌表中时,我们也更新 local_cost 的值,此时,我们选择的特赦条件为 cost < global_cost。当我们遍历完 y 的所有邻居时,我们 local_cost 的值进行判定:如果 local_cost == DBL_MAX,那么代表当前 y 的所有邻居都无法通过贪心算法求出解,此时我们不需进行回溯,而是直接跳出循环;local_cost < global_cost 时,我们更新 global_cost、global_x、global_y 的值;否则,不进行任何操作。完成判定后,我们把当前 y 更新成局部最优 y,即 local_y,并把 local_y 编码加入到 ts 中。在算法中,我们使用 unordered_set <string> 来保存禁忌条目,通过独热编码的形式来表示不同的禁忌。
pair<double, double> Solver::tabu() {
if (!Solver::load()) {
return make_pair(-1.0, -1.0);
}
int T = 100;
struct timeb t0, t1;
ftime(&t0);
double global_cost = Solver::greedy(false).first;
if (global_cost < 0) {
cerr << "Failed to solve with greedy" << endl;
return make_pair(-1.0, -1.0);
}
vector<int> global_y = this->y;
vector<vector<int>> global_x = this->x;
while (T-- != 0) {
double local_cost = DBL_MAX;
vector<int> local_y = this->y;
vector<vector<int>> local_x = this->x;
for (int i = 0; i < this->nfacility; ++i) {
this->y[i] ^= 1;
pair<double, double> result = Solver::greedy(false);
if (result.first >= 0 && ((result.first < local_cost && ts.find(Solver::encode(this->y)) == ts.end()) || (result.first < global_cost))) {
local_cost = result.first;
local_y = this->y;
local_x = this->x;
}
this->y[i] ^= 1;
}
if (local_cost == DBL_MAX) {
break;
} else if (local_cost < global_cost) {
global_cost = local_cost;
global_y = local_y;
global_x = local_x;
}
this->y = local_y;
this->x = local_x;
this->ts.insert(Solver::encode(local_y));
}
ftime(&t1);
string status = "";
for (int i = 0; i < this->nfacility; ++i) {
if (global_x[i].empty()) {
status += "0 ";
} else {
status += "1 ";
}
}
string path = "Results/p" + to_string(this->sn);
ofstream fout(path);
fout << fixed << setprecision(1) << global_cost << endl;
fout << status << endl;
for (int i = 0; i < this->nfacility; ++i) {
fout << global_x[i] << endl;
}
fout.close();
return make_pair(global_cost, (t1.time-t0.time)+(t1.millitm-t0.millitm)*1e-3);
}
实验结果保存在以下文件夹中。
简略的结果表保存在以下文件中。
Comparison
通过比较 Greedy 和 Tabu 的结果,我们能发现 Tabu 在每个实例上都能取得比 Greedy 好的数据,且时间开销平均仅不到 Greedy 的一千倍(每个实例不超过 0.5s)。在某些实例上,Tabu 得到方案的开销仅为 Greedy 的一半左右,则证明使用 Tabu 要远优于使用 Greedy。最后,项目的全部文件保存在以下文件夹中,更详细的结果可在 github 上查看。